Representation is one of the most complex and compelling tasks in machine learning. The way we represent facts, events, objects, labels, etc., affects how an autonomous learning agent can analyse them, extract insights, make predictions, and deliver knowledge.
In this blog post, we focus on natural language processing and on how to represent textual entities such as words, sentences, paragraphs, or entire documents. Dealing with text is hard because, from the “algorithm” perspective, it is just a list of strings or characters. If we want to grab text and use it in various analytics tasks efficiently, we need to find simple, meaningful representations that a machine and the algorithms that run on it can understand.
There are several approaches to deal with this challenge. This blog post presents techniques for representing text as a vector. Such representation allows not only to make “mathematical” operations but also to compute distance/similarity. The concepts of similarity and dissimilarity are widely employed in artificial intelligence. They have several applications in data mining, information retrieval, and pattern matching. In our case, we use similarities as a graph-construction technique.
Graphs of documents, paragraphs, sentences and words can be created using vector representation and similarity functions. Once the graph is created, link analysis and other graph-specific algorithms can be applied on top of such graphs. Text summarisation, for instance, can be implemented by applying PageRank to the sentence graph.
The better the vector representation, the better the similarity and hence the accuracy of the algorithm deployed on top of it.
Document embeddings
Using raw text in machine learning algorithms can be approached from various perspectives. It can be as simple as representing documents as a bag-of-words (BOW), that is, as an unordered collection of individual words disregarding grammar and the relative position in the document. In this approach, documents are encoded as sparse vectors, where each dimension corresponds to a word in the corpus and the value is its document frequency. This model can be extended by using TF-IDF instead of document frequency, where TF is a term frequency (how often that word occurs in the current document) and IDF is an inverse document frequency (the more frequent corpus-wise, the less important it is). Despite their simplicity, these traditional methods are sufficient for many use cases. However, this representation generates very long and sparse vectors, which suffer from several shortcomings: near-orthogonality between vectors, an inability to account for context and word order, and an inability to capture the document’s deeper semantic meaning.
What’s out there?
Embeddings are dense vector representations of words or whole documents. They are trained, typically using neural networks, to capture the contextual and semantic meaning of text, which can then be used as input to subsequent complex machine learning algorithms, such as neural networks for sentiment analysis.
There are various approaches and countless possible implementations. One of the traditional ones is using so-called autoencoders: deep neural networks which are being forced, by introducing into their internal design a bottleneck layer (see figure) with a much lower dimension than the input, to learn a dense low-dimensional representation of the input document (represented as a sparse BOW vector) which captures its deeper semantic meaning [1].
![Schematic structure of an autoencoder. [2] Schematic structure of an autoencoder. [2]](https://graphaware.com/wp-content/uploads/2024/09/Autoencoder_structure.png)
Concrete implementations can include Stacked Restricted Boltzmann Machines (RBMs), Variational Autoencoders (VAEs), or even Convolutional Neural Networks (best known for image classification tasks).
Deep neural networks are not always the best solution. They can introduce unnecessary complexity, resulting in excessive demands on computational power and training data.
On the other hand, shallow neural network models for word and document embeddings have gained significant momentum in recent years. Rather than complexity, they bet on simplicity because there are no hidden layers. This enables them to be deployed more efficiently on larger datasets, resulting in better overall performance than more complex models. An example of such an approach is word2vec [3] for word embeddings, and its extended version, Paragraph Vectors [4], which is also known as doc2vec, for document embeddings.
We focus here on the latter, as it is most suitable for representing an entire document, and the training process can be customised to support document classification.
Paragraph vectors
Basic concepts
Document embeddings were introduced in [4], where two distinct approaches were presented: Distributed Memory (PV-DM) and Distributed Bag of Words (PV-DBOW).
DM works as follows (see figure below):
- Each word is assigned a random vector of specified dimension
- A unique ID represents each document (paragraph) and has its own vector
- Sliding window algorithm scans through documents (sliding window size represents a context window)
- Word and document vectors are concatenated or averaged and used in a softmax classifier to predict the next word
- Stochastic gradient descent is used to train the vectors and softmax classifier parameters
![Architecture of Paragraph Vectors - Distributed Memory [4] Architecture of Paragraph Vectors - Distributed Memory [4]](https://graphaware.com/wp-content/uploads/2024/09/doc2vec-DM.png)
The PV-DBOW architecture operates in a very similar fashion, except that the vector representing a paragraph (document) is trained to predict a sequence of words within a small window (see figure below). This model is simpler and requires storing only softmax weights, whereas PV-DM also requires storing word vectors. Le and Mikolov [4] found that PV-DM consistently outperforms PV-DBOW, but that the best performance across many tasks is achieved when the two vectors are concatenated.
![Architecture of Paragraph Vectors - Distributed BOW [4] Architecture of Paragraph Vectors - Distributed BOW [4]](https://graphaware.com/wp-content/uploads/2024/09/doc2vec-BoW.png)
Paragraph Vectors allow us to represent a document as vectors of the overall topics. The learning algorithms capture the semantic content of documents and can serve as input to other machine learning tasks, rather than the overly simplistic and very sparse BOW vectors. Moreover, just like word vectors, they do behave like real vectors: they can be used in linear translations with other embeddings, including word2vec vectors [5]. For instance:
- vec(Japan) – vec(Sushi) + vec(Germany) ≈ vec(bratwurst)
- vec(Einstein) – vec(scientist) + vec(Picasso) ≈ vec(painter)
- vec(Berlin) – vec(Germany) + vec(France) ≈ vec(Paris)
Implementation
There are various implementations available; for example, Gensim is a Python library that performs the heavy lifting in the background in C. We have, however, chosen the DeepLearning4J library, which allows us to integrate such features seamlessly into GraphAware Hume on top of Neo4j.
The algorithm can be fed with full documents represented as strings (in which case it performs very basic tokenisation and only trivial, pattern-based lemmatisation internally). Here is an example of the procedure call in Hume to train a new model:
CALL ga.nlp.vector.train({type:'doc2Vec', parameters:{query: "MATCH (n:Train) WHERE length(n.text) > 10 WITH n, rand() as r ORDER BY r RETURN n.text as text, id(n) as docId", iterations: 15, epochs: 10, layerSize: 400}}) YIELD result
return result
Note that we use rand() Cypher random number generator function to ensure that documents are shuffled between epochs (neural networks are good at memorizing training data, let’s make that harder for them). To use the trained model to get and store embedding vectors for the entire document, run:
CALL apoc.periodic.iterate('MATCH (s:Wikipage) WHERE length(s.text) > 10 return s',
"CALL ga.nlp.vector.compute({node: s,
type:'doc2Vec',
property:'doc2vec_dim400',
label:'Doc2VecContainerSentence',
parameters: {query:'MATCH (n:HandPicked) WHERE id(n) = {id} RETURN n.text as text', iterations: 10, useExistingAnnotation: False}})
YIELD result
return result", {batchSize: 10, parallel: false})
Alternatively, we can create our own annotations (leveraging, for example, Stanford CoreNLP) and feed it already tokenized and lemmatized tags. This allows for instance to define a better vocabulary used then during the training phase.
CALL ga.nlp.vector.train({type:'doc2Vec', parameters:{query: "match (n:Train)-[:HAS_ANNOTATED_TEXT]->(a:AnnotatedText)-[:CONTAINS_SENTENCE]->(:Sentence)-[:SENTENCE_TAG_OCCURRENCE]->(to:TagOccurrence)-[:TAG_OCCURRENCE_TAG]->(t:Doc2VecVocabulary) with n, t, to order by to.startPosition asc return id(n) as docId, collect(t.value) as tokens", iterations: 15, epochs: 5, layerSize: 400, useExistingAnnotation: True}}) YIELD result
return resultThe vocabulary (in the query above represented by tags with label Doc2VecVocabulary) can be constructed, for example, in this way:
match (:Train)
with count(*) as total_docs
match (:Train)-[:HAS_ANNOTATED_TEXT]->(a:AnnotatedText)-[:CONTAINS_SENTENCE]->(:Sentence)-[r:HAS_TAG]->(t:Tag)
with t, count(distinct a) as n_docs, sum(r.tf) as sum_tf, total_docs
where n_docs > 1 and n_docs * 1.0/total_docs < 0.4
with t
order by n_docs desc, sum_tf desc
limit 700000
set t:Doc2VecVocabularyFor constructing and storing embedding vectors, use the same query as for vectors from strings, but set the useExistingAnnotation parameter to True and change the query to:
MATCH (n:Wikipage)-[:HAS_ANNOTATED_TEXT]->(a:AnnotatedText)-[:CONTAINS_SENTENCE]->(:Sentence)-[:SENTENCE_TAG_OCCURRENCE]->(to:TagOccurrence)-[:TAG_OCCURRENCE_TAG]->(t:Tag) WHERE id(n) = {id} with to, t order by to.startPosition asc return t.value as tokenEvaluation
The main purpose of the vector representation is to create a proper similarity graph model of the documents or sentences. Hence, to evaluate the quality of the vectors, we have to evaluate the extent to which they are capable of capturing similarity and dissimilarity between documents. We followed the approach in [5] and used Wikipedia page triplets to evaluate and test the similarity. The idea is to gather three Wikipedia articles, two of which are of a very similar topic, one that is of a different (less related) topic, and use doc2vec embedding vectors to decide which of the two articles is more similar based on cosine similarity. For example, articles about Deep Learning and Machine Learning are more similar to each other than to an article about computer networks.
The dataset consists of two sets of triplets: 172 hand-picked triplets and almost 20000 automatically generated triplets (two articles are from the same category, one is from a different – potentially sibling – category). We scraped and ingested all of them into Neo4j, used the automatically generated triplets as a training dataset, and the handpicked ones for evaluation. Despite a relatively small training dataset (for comparison, the original paper [4] used the full Wikipedia, i.e., ~4.5M pages, and the paper [5] used ¼ of Wikipedia), the results are encouraging. Our achieved accuracy exceeds that reported in [5] and is close to that reported in [4].
The table below contains results for some of our experiments with Paragraph Vectors. We conducted multiple tests to assess the effects of parameters such as vector dimension, learning rate, number of iterations, epochs, and window size on the final quality. The highest accuracy was achieved with a vector dimension of 800, a learning rate of 0.025, and 15 iterations (10 epochs). However, this comes at the cost of a serialised model size (9.3 GB) and increased training time and resource requirements (8 hours on a single cloud server with 16 cores and 64 GB of RAM). A reasonable alternative is to reduce the dimensionality to 400, which has approximately 2% lower accuracy and took approximately 2.5 h to compute.
| Dim | Learn. rate | Iter | Epochs | Window | Model size (GB) | Accuracy |
|---|---|---|---|---|---|---|
| 200 | 0.025 | 10 | 10 | 5 | 2.4 GB | 75% |
| 400 | 0.001 | 10 | 10 | 5 | 4.7 GB | 79.6% |
| 400 | 0.001 | 15 | 10 | 5 | 4.7 GB | 82.6% |
| 400 | 0.001 | 15 | 5 | 5 | 4.7 GB | 79.1% |
| 400 | 0.025 | 15 | 5 | 5 | 4.7 GB | 84.3% |
| 400 | 0.025 | 15 | 5 | 8 | 4.7 GB | 83.7% |
| 800 | 0.001 | 15 | 10 | 5 | 9.3 GB | 84.9% |
| 800 | 0.025 | 15 | 10 | 5 | 9.2 GB | 86.6% |
We also tested the influence of sliding window size. In the case of dimension 400, increasing the window from 5 to 8 resulted in a 0.6% decrease in accuracy. However, it’s important to note that this difference is not statistically significant. As with any other neural network, the important part of the algorithm is the stochastic gradient descent. Therefore, by definition, the procedure is random, and we can obtain slightly different results each time we run it. After a couple of experiments like that, we observed that the reported accuracy has an uncertainty of approximately 2-3%. The observed difference between window sizes 5 and 8 is therefore irrelevant.
DL4J implementation of Paragraph Vectors also allows us to use a custom dictionary. We therefore utilised Stanford CoreNLP within our NLP framework to annotate all Wikipedia triplets and select the most relevant words as a dictionary (words occurring at least twice in the corpus and with document frequency below 40%). Thanks to this superior annotation procedure, we obtained a smaller vocabulary, resulting in better training performance (smaller model size, less training time), while maintaining the same accuracy.
Finally, it should be noted that the reported accuracies are also influenced by the number of iterations used during inferring document vectors from the trained model. By default, it uses the same total number of iterations as during training (i.e., the number of epochs multiplied by the number of iterations). That results in very slow inference. We, however, observed that using 10 iterations doesn’t deteriorate accuracy by more than ~0.5% (well within the accuracy uncertainty discussed above). Going even lower, to 1 iteration, makes inference approximately 10x faster, but at the expense of accuracy (a ~6% drop for vector dimension 800). The difference between the accuracies obtained with 10 and 5 iterations is again approximately 0.5%. We therefore conclude that the optimal settings require at least 5 inference iterations.
It is always useful to compare these results to some simple benchmark. We used cosine similarity of tf-idf vectors (sparse bag-of-words vectors with each element representing the tf-idf value of the word) instead of Paragraph Vectors, which gave us an accuracy of 77.9%. With Doc2vec, we achieved an almost 9% accuracy gain with a relatively modest training dataset (60k Wikipedia articles).
Visualisation of document embeddings
Given the amount of data processed, it is useful to find a way to represent the results of the analysis visually using a specific technique. As stated before, representing objects as vectors allows us to make different kinds of analyses and visualisations on them. One of them is described here. When we want to visualise high-dimensional data (such as Paragraph Vectors), we need to choose some dimensionality reduction technique to move from high-dimensional space to 2D (potentially 3D) space. The most popular ones are Principal Component Analysis (PCA) and t-SNE.
PCA is a statistical technique that finds such an orthogonal transformation of our original possibly correlated variables that best preserves the variance in our data, omitting possibly correlated variables and preserving those that represent the most informative viewpoint on the dataset.
t-SNE is another very useful algorithm for visualising high-dimensional data. It adapts to the underlying data by performing different non-linear transformations on different regions. This produces beautiful plots with well-separated clusters, but beware: as a result, the interpretation can sometimes be misleading. The notion of distance is adapted based on regional density variations in the dataset: it tends to expand dense clusters and contract sparse ones, making the relative cluster size meaningless. Similarly, cluster distances in t-SNE plots may mean nothing, just as random noise can, for some parameter choice, produce clusters! It is therefore important to always do a scan through the t-SNE parameter space (especially perplexity) to get a better feeling of what is going on. This is a very good article about the pitfalls of t-SNE [6].
For very high-dimensional data, it is often best performance-wise to combine both approaches: use PCA for reducing dimension to ~50 and then let t-SNE do its magic! This is the approach we chose, and the result for the full 120k Wikipedia dataset (we ingested 120k articles of specific categories and their subcategories) is shown in the following figure.
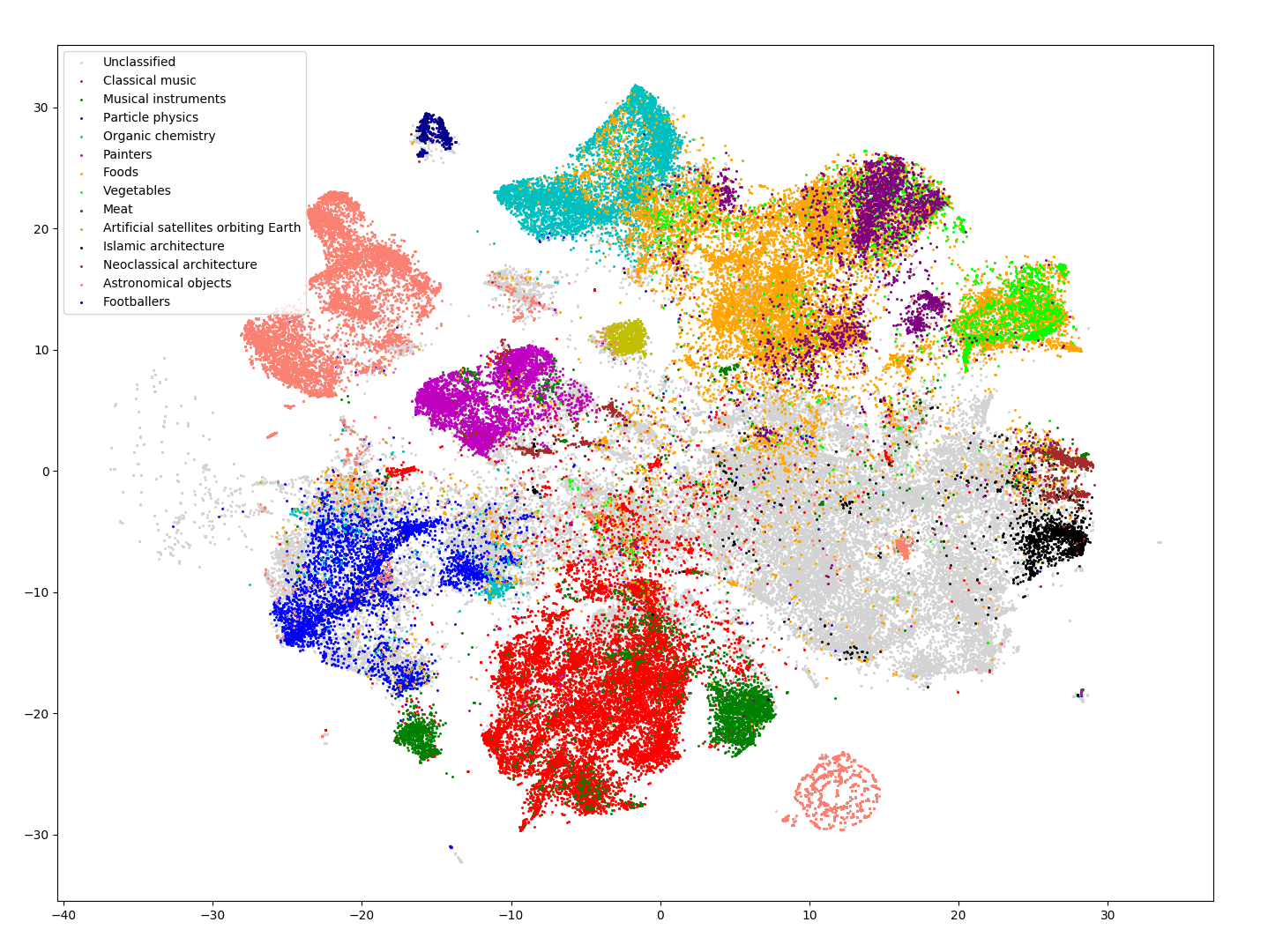
We can clearly see multiple well-defined clusters in our dataset, for example, Astronomical objects, Particle physics, Food, Painters, and Classical music. Some of the larger clusters are spread over a wider area. This can be attributed to too broad topics being included in one category. For example, Foods are overlaid with subcategories such as Vegetables and Meat (and others such as Food additives and* Food ingredients), which are quite distinctive for themselves. Similarly, for *Musical instruments: they are visualised as two independent clusters, the smaller one being a subcategory of Electronic musical instruments. Finally, the large grey blob is a combination of three categories: Countries of Europe / Asia / Africa. These appear to be too vague to create three distinct clusters.
Conclusions
In this blog post, we discussed the importance of a proper document representation. Rather than using the sparse BOW or TF-IDF vectors, we carefully tested and implemented (in GraphAware Hume) the Paragraph Vectors algorithm. Such a dense document embedding technique is useful for many other advanced machine learning tasks, and specifically as an intermediate step for building a significance graph from text of any size.
This blog post also highlights all the effort the GraphAware Hume team spent on:
- Defining a specific purpose (for instance, graph creation for text summarisation)
- Selecting a subset of algorithms to evaluate (autoencoders, Paragraph Vectors)
- Implementing, testing and evaluating all of them to find the strengths and weaknesses of each of them
- Explain the selected algorithms and the related features
- Further investigate for possible improvements or further usages
Here, in the first step, we demonstrated that even in a relatively modest corpus size, the embeddings produce meaningful results and can be useful in grouping documents of similar topics together, simplifying contextual similarity evaluation among various texts. In one of the next blog posts, we will see how they can be leveraged for machine learning classification algorithms.
Bibliography
[1] Hinton G, Salakhutdinov R., “Reducing the Dimensionality of Data with Neural Networks”, Science 2006; 313(5786): 504 – 507, https://www.cs.toronto.edu/~hinton/science.pdf
[2] Wikipedia, “Autoencoder”, https://en.wikipedia.org/wiki/Autoencoder
[3] T. Mikolov, K. Chen, G. Corrado, J. Dean, “Efficient Estimation of Word Representations in Vector Space”, arXiv:1301.3781 [cs.CL]
[4] Q. Le, T. Mikolov, “Distributed Representations of Sentences and Documents”, arXiv:1405.4053 [cs.CL]
[5] A. M. Dai, Ch. Olah, Q. V. Le, “Document Embedding with Paragraph Vectors”, arXiv:1507.07998 [cs.CL]
[6] https://distill.pub/2016/misread-tsne/


