Introduction: The Power of Graph Traversal
Imagine navigating through a vast social network to find the shortest path between two friends or determining the most efficient route between cities on a map. These real-world scenarios rely heavily on graph traversal techniques. Graph traversal is a fundamental concept in computer science that involves visiting all the nodes in a graph in a systematic manner to explore relationships and connections.
At its core, graph traversal is about exploring the nodes (or vertices) and edges of a graph to uncover patterns, detect cycles, find shortest paths, and more. This process is essential in various applications ranging from artificial intelligence and data analysis to database management and network design.
There are several graph traversal algorithms, each with its unique characteristics and use cases. Some of the most prominent ones include Breadth-First Search (BFS), Depth-First Search (DFS), Dijkstra’s Algorithm, Kosaraju’s Algorithm, and Tarjan’s Algorithm. Understanding these algorithms and their applications is crucial for anyone looking to leverage graph traversal in solving complex problems.
In this comprehensive guide, we will delve into the fundamentals of graph traversal, explore various algorithms in detail, and examine their practical applications across different domains. Whether you’re a seasoned developer or a computer science enthusiast, this article will equip you with the knowledge and skills to master graph traversal.
Understanding Graphs: A Foundation for Traversal
What is a Graph?
A graph is a mathematical structure used to model pairwise relations between objects. It consists of two primary components:
- Vertices (Nodes): The fundamental units or points in a graph.
- Edges: The connections or lines that link pairs of vertices.
Graphs can be categorized based on the direction of edges:
- Directed Graphs: Edges have a direction, indicating a one-way relationship.
- Undirected Graphs: Edges have no direction, indicating a two-way relationship.
Types of Graphs
Graphs come in various types, each suited for different applications:
- Weighted Graphs: Edges carry weights representing cost, distance, or other metrics.
- Unweighted Graphs: Edges do not carry any additional information.
- Cyclic Graphs: Graphs that contain cycles, where a path starts and ends at the same vertex.
- Acyclic Graphs: Graphs without cycles, such as trees and Directed Acyclic Graphs (DAGs).
Graph Representation
Efficiently representing a graph in code is crucial for optimizing traversal algorithms. The two most common representations are:
- Adjacency Matrix: A 2D array where each cell
matrix[i][j]indicates the presence (and possibly the weight) of an edge between verticesiandj. - Adjacency List: An array or list where each index represents a vertex and contains a list of its adjacent vertices.
Why Graph Representation Matters
The choice of graph representation significantly impacts the efficiency of traversal algorithms. While adjacency matrices allow constant-time edge checks, they consume more space, especially for sparse graphs. Adjacency lists, on the other hand, are more space-efficient for sparse graphs but may require more time to check for the existence of specific edges.
Choosing the right representation based on the graph’s characteristics and the application’s requirements can lead to substantial performance improvements.
Navigating through the graph’s nodes and edges
Graph databases are a type of NoSQL database that use graph structures with nodes, edges, and properties to represent and store data. They are designed to handle highly connected data and are optimized for traversing relationships. This makes them particularly suited for applications such as social networks, recommendation engines, and fraud detection. Unlike traditional relational databases, which require complex joins to navigate relationships, graph databases allow for direct connections between data points, resulting in faster and more efficient queries. This is especially beneficial when dealing with large datasets where performance is a critical factor.
In a graph database, a graph traversal is a fundamental operation that involves navigating through the graph’s nodes and edges to retrieve or manipulate data. This process is typically performed using a query language, such as Cypher in Neo4j, that allows developers to specify the starting point of the traversal, the direction in which to navigate (incoming, outgoing, or both), and any conditions that need to be met along the way. Graph traversals can be simple, such as finding all friends of a user in a social network, or complex, involving multiple hops and filters to discover hidden patterns or relationships. The efficiency of graph traversals is one of the key advantages of using graph databases, as they can quickly navigate large and dense networks of data without the need for expensive joins or lookups.
Breadth-First Search (BFS): Exploring Level by Level
What is BFS?
Breadth-First Search (BFS) is a graph traversal algorithm that explores nodes level by level, starting from a given source node. It systematically visits all neighbors of the current node before moving to the next level of nodes. BFS is particularly effective in finding the shortest path in unweighted graphs
BFS Applications
- Finding the Shortest Path: In unweighted graphs, BFS can efficiently find the shortest path between two nodes.
- Network Broadcasting: BFS can be used to simulate the broadcasting of information across a network.
- Web Crawling: Search engines utilize BFS to crawl the web systematically.
BFS Complexity Analysis
The time complexity of BFS is O(V + E), where V is the number of vertices and E is the number of edges. The space complexity is also O(V), due to the storage required for the queue and the visited array.
Depth-First Search (DFS): Diving Deep into Connections
What is DFS?
Depth-First Search (DFS) is a graph traversal algorithm that explores as far as possible along each branch before backtracking. Unlike BFS, which explores nodes level by level, DFS dives deep into the graph, making it suitable for scenarios where exploring the full depth of a graph is necessary.
DFS Applications
- Detecting Cycles: DFS can be used to detect cycles in both directed and undirected graphs.
- Topological Sorting: In DAGs, DFS is instrumental in performing topological sorts.
- Pathfinding (Maze Solving): DFS can explore all possible paths in maze-like structures.
DFS Complexity Analysis
The time complexity of DFS is O(V + E), where V is the number of vertices and E is the number of edges. The space complexity is O(V), due to the recursion stack (in recursive implementations) or the explicit stack used in iterative implementations.
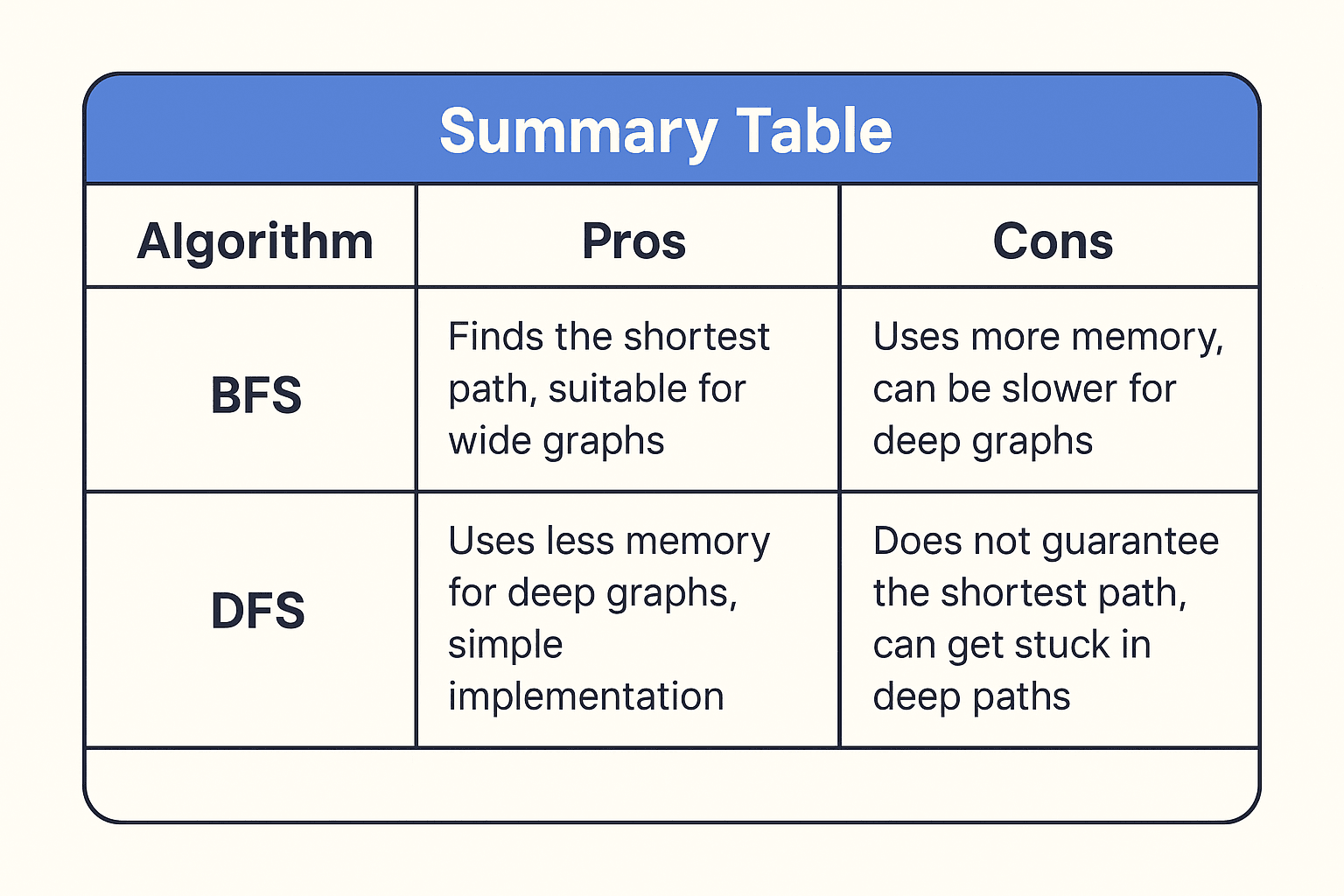
BFS vs. DFS: Choosing the Right Algorithm
Key Differences
| Aspect | Breadth-First Search (BFS) | Depth-First Search (DFS) |
|---|---|---|
| Exploration Strategy | Level by level | Deepest nodes first |
| Data Structure Used | Queue | Stack (or recursion) |
| Memory Usage | Requires more memory for wide or large graphs | Generally uses less memory for deep or sparse graphs |
| Shortest Path | Finds the shortest path in unweighted graphs | Does not guarantee the shortest path |
| Applications | Shortest path, web crawling, network broadcasting | Cycle detection, topological sorting, maze solving |
When to Use BFS
- When the shortest path in an unweighted graph is needed.
- In scenarios requiring exploration of nodes closest to the source first, such as web crawlers or social network connections.
- For applications like network broadcasting where information needs to propagate level by level.
When to Use DFS
- When exploring all possible paths or configurations is necessary, such as puzzle solving or pathfinding in mazes.
- For tasks like cycle detection, topological sorting, and identifying strongly connected components.
- When memory usage is a constraint, especially in deep or sparse graphs.
Summary Table
Advanced Graph Traversal Algorithms
Dijkstra’s Algorithm
Dijkstra’s Algorithm is a graph traversal algorithm used to find the shortest paths between nodes in a weighted graph. Unlike BFS, which works on unweighted graphs, Dijkstra’s Algorithm accounts for edge weights, making it suitable for a broader range of applications.
Kosaraju’s Algorithm
Kosaraju’s Algorithm is designed to find strongly connected components (SCCs) in directed graphs. A strongly connected component is a subgraph where every vertex is reachable from every other vertex in the same subgraph.
Tarjan’s Algorithm
Tarjan’s Algorithm is another method for finding strongly connected components in a directed graph. It efficiently identifies SCCs in a single DFS traversal, making it more optimal in certain scenarios compared to Kosaraju’s Algorithm.
Practical Applications of Graph Traversal
Recommendation Systems
Graph traversal plays a pivotal role in recommendation systems by analyzing user connections and preferences. By traversing the graph of users and items, algorithms can identify patterns and suggest products, movies, or friends that align with a user’s interests.
Search Engines
Search engines utilize graph traversal to crawl the web and index websites efficiently. BFS is often employed to ensure that all pages are discovered systematically, enabling the creation of comprehensive search indexes.
Social Network Analysis
In social networks, graph traversal helps analyze networks and social connections, identify communities, and detect influencers. Algorithms like BFS and DFS can uncover hidden relationships and measure the strength of connections within the network.
AI and Machine Learning
Graph traversal techniques are integral to various AI applications, including knowledge graphs, reasoning, and planning. They enable AI systems to navigate complex relationships and make informed decisions based on interconnected data.
Graph Traversals in Criminal Data Analysis
Graph traversals play a crucial role in criminal data analysis, enabling law enforcement agencies to efficiently uncover and interpret complex relationships within vast datasets. By leveraging the power of graphs, investigators can quickly identify connections between individuals, locations, and events, leading to more effective crime-solving strategies. Graph technology offers several advantages in this domain:
- Relationship-centric insights: Criminal networks are inherently relational. Graphs provide a natural representation, allowing for intuitive analysis of connections between suspects, victims, and criminal activities.
- Rapid pattern detection: Using graph traversals, analysts can swiftly identify patterns indicative of criminal behaviour, such as money laundering or drug trafficking routes.
- Scalability: As criminal data grows, graph databases can scale efficiently, maintaining performance while accommodating increasing amounts of data.
- Advanced algorithms: Graph technology supports sophisticated algorithms, such as community detection and centrality measures, which can provide deeper insights into criminal networks.
In summary, graph traversals are invaluable in criminal data analysis, offering a robust framework for uncovering hidden connections and patterns that traditional data analysis methods may overlook.
How Traversals Power GraphAware Hume
In Hume, graph traversals are the engine that drives discovery, automation, and analysis. They turn a static dataset into a dynamic and explorable knowledge system.
1. Contextual Search and Discovery
Hume lets analysts ask questions of the graph—e.g., “Show me all entities linked to this person within 3 degrees.” This is powered by traversals under the hood, often with constraints like relationship types, timeframes, or properties.
2. Automated Workflows (Hume Orchestra)
Hume allows users to define automated workflows that include custom graph traversals—e.g., find all connected entities within a fraud ring and enrich them with open-source intelligence (OSINT). This enables semi-autonomous investigations.
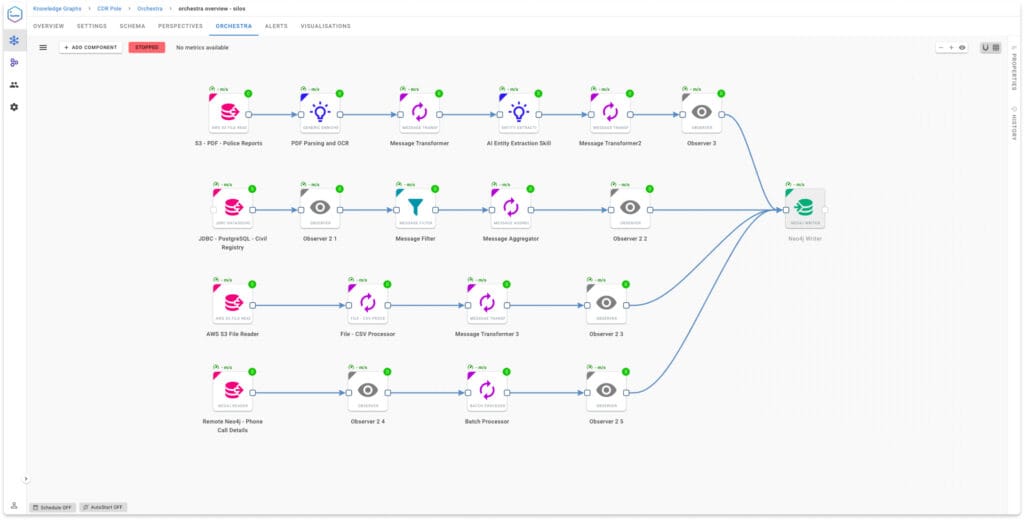
3. Graph-Powered Visualizations
The visual interface lets analysts click into nodes and expand their neighborhoods—which triggers live traversals in real time, helping them follow leads dynamically.
4. Pattern Detection and Intelligence Use Cases
Traversals are core to detecting patterns like:
- Money laundering chains
- Terrorist network structures
- Procurement fraud loops
These patterns are often expressed as reusable traversal templates within Hume.
5. LLM-Driven Queries (Hume LLM Integration)
Even when an analyst uses natural language, like “Find all companies indirectly owned by X,” Hume’s LLM layer translates that into a graph traversal—bridging the gap between human reasoning and graph logic.
Optimizing Graph Traversal Performance
Data Structures
The choice between adjacency lists and adjacency matrices can significantly impact traversal performance. Adjacency lists are generally more space-efficient for sparse graphs and allow faster iteration over neighbors. In contrast, adjacency matrices provide quicker edge existence checks but consume more memory, making them suitable for dense graphs.
Visited Node Tracking
Efficiently tracking visited nodes is crucial to prevent infinite loops and redundant processing. Using structures like boolean arrays or hash sets ensures that each node is visited only once, enhancing traversal efficiency.
Parallel Processing
For very large graphs, parallel processing can be employed to speed up traversal. Dividing the graph into smaller subgraphs and processing them concurrently can significantly reduce traversal time, especially in distributed systems and multi-core environments.
Conclusion: Mastering the Art of Graph Exploration
In this comprehensive guide, we delved into the core concepts of graph traversal, explored essential algorithms like BFS and DFS, and examined their practical applications across various domains. We also touched upon advanced algorithms and optimization techniques that enhance traversal performance.
Graph traversal remains a fundamental skill for computer scientists and software engineers alike. By mastering these techniques, you can tackle complex problems, build innovative solutions, and leverage the full potential of graph-based data structures.
We encourage you to experiment with the provided code examples, apply these algorithms to real-world scenarios, and continue exploring the vast landscape of graph theory and its applications.
